Obiettivo: Determinare il valore di un integrale definito utilizzando il metodo dei rettangoli e sfruttando il software di calcolo numerico Scilab.
Il metodo dei rettangoli:
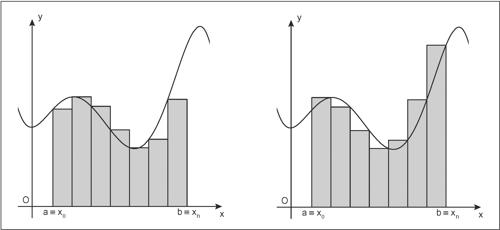
Il metodo dei rettangoli, o somme di Riemann, è un approccio numerico per approssimare l’integrale definito di una funzione su un intervallo [a, b]. È uno dei metodi più semplici per comprendere l’integrazione come somma di aree.
L’idea alla base di questo approccio è quella di suddividere l’intervallo [a,b] in n sotto-intervalli di ampiezza costante h=(b−a)/n. Su ciascun sottointervallo, si costruisce un rettangolo la cui altezza dipende dal valore della funzione in un punto scelto del sottointervallo.
Codice:
Un esempio del metodo dei rettangoli viene effettuato utilizzando il seguente codice Scilab il quale ha l’obiettivo di determinare il valore dell’integrale definito nell’intervallo [0, 2] della funzione
y = x^2
Esercizi:
Graficare le seguenti funzioni utilizzando il software di calcolo numerico Scilab:
- y = 1 nell’intervallo [0, 2]
- y = cos(x) nell’intervallo [0, pi/2]
- y = x*ln(x) nell’intervallo [1, 2]